Os tubos de cana ou de outras plantas de tronco oco, constituíram os primeiros instrumentos musicais. Emitiam som soprando por um extremo. O ar contido no tubo entrava em vibração emitindo um som.
As versões modernas destes instrumentos de sopro são as flautas, as trombetas e os clarinetes, todos eles desenvolvidos de forma que o intérprete produza muitas notas dentro de uma ampla gama de freqüências acústicas.
O órgão é um instrumento formado por muitos tubos nos quais cada tubo da uma só nota.
O tubo de órgão é excitado pelo ar que entra pelo extremo inferior. O ar se transforma em um jato na ranhura entre o corpo (uma placa transversal ao tubo) e o lábio inferior. O jato de ar interage com a coluna de ar contida no tubo. As ondas que se propagam ao longo da corrente turbulenta mantém uma oscilação uniforme na coluna de ar fazendo com que o tubo soe.
Ondas estacionárias nos tubos
Tubos Abertos: os tubos abertos possuem uma extremidade oposta à embocadura, ou seja, a entrada do ar aberta. A onda estacionária se forma no ar de seu interior, quando o tubo aberto ressoa.
Nas duas extremidades do tubo, ou seja, na embocadura e na extremidade aberta, há uma formação de ventres, isto é, uma interferência construtiva.
Vejamos uma figura abaixo, onde podemos perceber que estão representadas as três primeiras ondas estacionárias, que poderão aparecer na coluna de ar do interior de um tubo aberto que contenha um comprimento útil igual a L. Veremos abaixo os três modos de vibração que correspondem ao 1º, 2º e 3º harmônico:
Considerando  o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos:
o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos:
Considerando V, como sendo o módulo da velocidade das ondas parciais, onde elas se superpõem para que haja formação das ondas estacionárias e fn, a freqüência de um harmônico de ordem n, vem:
Tubos Fechados: Os tubos fechados possuem uma extremidade oposta a embocadura, ou seja, a entrada do ar fechada. A onda estacionária se forma no ar de seu interior, quando o tubo fechado ressoa.
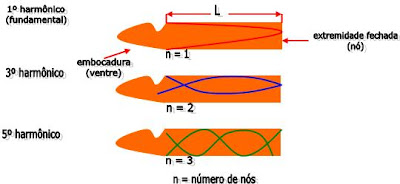
Podemos perceber que junto à embocadura, há formação de um ventre, ou seja, interferência construtiva, e junto à extremidade fechada, ocorre à formação de um nó, ou seja, interferência destrutiva.
Vejamos uma figura abaixo, onde podemos perceber que estão representadas as três primeiras ondas estacionárias, que poderão aparecer na coluna de ar do interior de um tubo fechado que contenha um comprimento útil igual a L. Veremos abaixo os três modos de vibração que correspondem ao 1º, 2º e 5º harmônico.
Considerando  o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos:
o comprimento da onda estacionária que está presente no tubo, esse comprimento poderá ser expresso em função de L. Em cada caso é dado de uma forma, vejamos:
Considerando V, como sendo o módulo da velocidade das ondas parciais, onde elas se superpõem para que haja formação das ondas estacionárias e f(2n – 1), a freqüência de um harmônico de ordem (2n -1), vem: